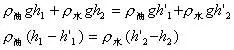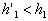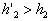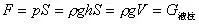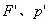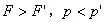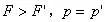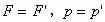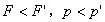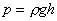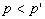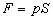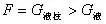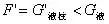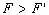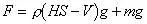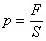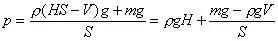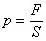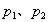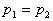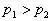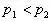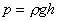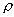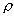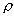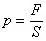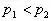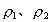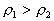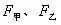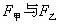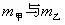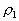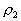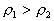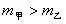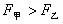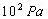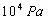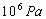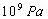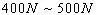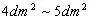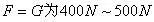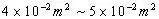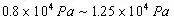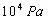初中压强题7种解题法

1. 整体法

以整体为研究对象，对于液面高度变化及不同液体混合等问题运用整体法解决较为方便。

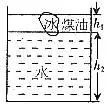
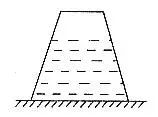
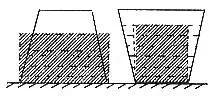
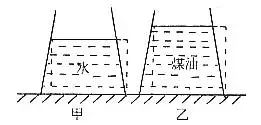
例、如图1所示，冰块浮在杯中水面上，且水面上覆盖有一层煤油。问：在冰完全熔化后，水面高度怎么变？油面厚度怎么变？

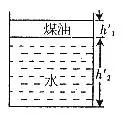
分析与解：以冰块、水、煤油构成的整体为研究对象，油层和水层的厚度如图1所示和如图2所示，由于整体总重力不变，此整体对同样的杯底的压强不变，故有：

故正确答案为：水面高度上升，煤油层厚度变薄。

2. 假设法

指在分析问题时，依据具体情况把问题中某个过程或条件假设为理想的物理过程或特殊条件，在此基础上进行分析，得出正确的结论。

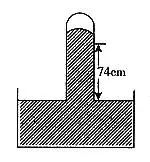
例、如图3所示，一同学测定大气压时，测得水银柱高度为74cm，若此时外界为一个标准大气压，当玻璃管倾斜放置时，则管内水银柱（   ）

A. 长度变长，高度不变

B. 长度、高度都不变

C. 长度变长，高度减小

D. 长度、高度都变大

分析与解：外界为一标准大气压，而水银柱高为74cm，则说明管中水银柱上方含有少量空气。当管倾斜放置时，假设水银柱长度不变，则水银柱高度变小。大气压对管中空气柱压强变大，空气柱体积变小，故水银柱长度变长。假设水银柱高度不变，则水银柱长度变长，空气柱长度变短，空气柱产生的压强变大，所以水银柱要下降，故高度减小，故正确答案为C。

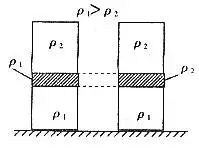
3. 等效法

                                            图5                图6

4. 隔离法

将研究对象从其所处的系统中隔离出来，分析和研究其所处的状态即受力情况等。利用隔离法解题要特别注意正确选取隔离体。

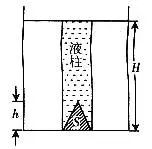
例、如图7所示，圆柱形容器内部底面上有一个锥形的凸出体（它与容器底是连在一起的）。若该锥体质量为m，高为h，体积为V，底面积为S，当容器中倒入密度为，深为的液体时，锥体对容器的压强为多大？

5. 割补法

6. 作图法

用作图法来直观的表示各物理量的关系，在解决某些问题时，利用作图法可以用帮助正确的认识物理过程，使抽象变具体，还能省去一些烦琐的运算。

7. 估算法

通过审题、分析与比较并能结合生活实际，对某些过程或某些物理量作出估算，再通过适当的运算，得出合适的答案。

这类问题的求解要抓住事物的主要因素，略去次要因素。

例、一个中学生双脚站在水平地面上，他对地面的压强值接近于（     ）

故正确答案为：B。

解题的关键是选择正确的解题方法，所以我们在平时的学习中要逐步培养勤于思考，善于总结，敢于分析，逐步培养良好的思维习惯，时时寻找最佳的解题方案，从而提高物理解题能力。

相关文章

• 2019年福建中考物理真题（附WORD打印版下载）
• 2019年广东中考物理真题（附WORD打印版下载）
• 2019年江西中考物理真题（附WORD打印版下载）
• 2019安徽中考物理真题（附WORD打印版下载）
• 2019河南中考物理真题（WORD打印版下载）
• 2019湖南衡阳市中考物理真题（打印版）
• 2019河北中考物理真题（附WORD打印版下载）
• 2019重庆中考物理真题（附打印版下载）
• 2019山东德州市中考物理真题（附WORD打印版下载）
• 睡的越来越晚，走的越来越往南方城市的原因分析